the magnetocaloric effect

 

Introduction

The Magnetocaloric Effect (MCE), discovered in 1881 by E. Warburg[1], is an exciting propriety of magnetic materials. This effect can be seen from either an adiabatic or an isothermal process; both due to a change of the applied magnetic field. Considering an adiabatic process, the magnetic material changes its temperature, whereas from an isothermal process, the magnetic material exchanges heat with a thermal reservoir. Figure 1 clarify these processes.

From the quantitative point of view, the MCE is measured trough the magnetic entropy change DS (=DQ/T, where DQ is the amount of heat exchanged between the thermal reservoir and the magnetic material), when the isothermal process is considered; or adiabatic temperature change DT, when the adiabatic process. These quantities can also be seen when the magnetic entropy is expressed as a function of temperature for both, with and without applied magnetic field. See figure 2.

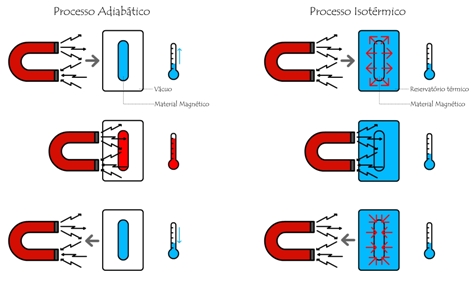
            Figure 1. Isothermal and Adiabatic processes. Dowload here a figure of higher quality.

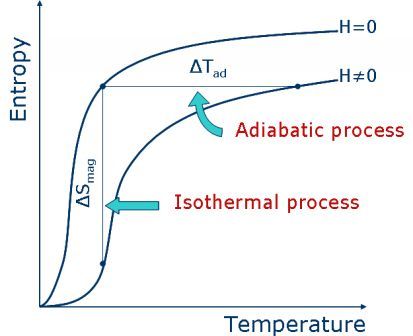
Figure 2. Magnetic entropy as a function of temperature for both: with and without applied magnetic field. Note the isothermal process (characterized by the magnetic entropy change DS) and the adiabatic process (characterized by the adiabatic temperature change DT).

It is straightforward the idea to produce a thermo-magnetic cycle based on the isothermal and/or adiabatic processes (like Brayton and Ericsson cycles - see figure 3); and indeed this idea begun in the late 1920s, when cooling via adiabatic demagnetization was proposed by Debye[2] and Giauque[3]. The process was after demonstrated by Giauque and MacDougall, in 1933; where they reach 250 mK[4]. Since then, the adiabatic demagnetization was used within some contexts; for instance, to cool NASA-XRS detectors (~1.5 K)[5]. On the other hand, room temperature magnetic cooling device technology is still in an early phase of development, with no commercially available products and only few prototypes. In August 2001, Astronautics Corporation of America, USA, announced a prototype of room temperature magnetic cooler. This machine has a cooling power of 95W, and uses as the active magnetic material Gd spheres[6]. Later, in March 2003, Chubu Electric and Toshiba, Japan, also announced a room temperature magnetic cooler prototype. This machine has a cooling power of 60W, and uses a layered bed of a Gd-Dy alloy as the active magnetic material[6].

 

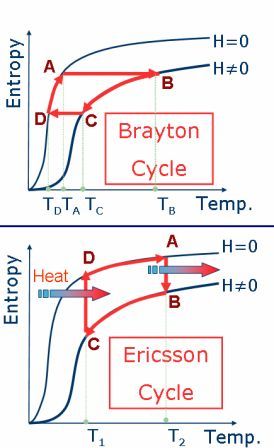
Figure 3. Thermo-magnetic cycles. Top: Brayton cycle, based on two adiabatic processes. Bottom: Ericsson cycle, based on two isothermal processes.

However, nowadays, the magnetic materials available and studied by the scientific community do not have yet the needed characteristics to be used in large scale, due to technological and/or economic restrictions. For a successful application, we need a material of low cost, non-toxic, good thermal conductivity and with a huge and broad DS vs. temperature (maximum around the magnetic phase transition). In this sense, most of the research developed world wide is devoted to explore and optimize the magnetocaloric properties of known materials, as well to seek for new magnetocaloric features in new materials.

In addition to the spin entropy, all of the mechanisms sensible to the magnetic field can be useful to maximize the DS, namely the lattice, charge and orbital entropies; since these entities, in certain cases, can also be ruled by the applied magnetic field. In this sense, some materials with strong electronic correlation have coupled magneto-structural transitions, maximizing the DS. An overview of the know materials is described in the Materials section.

            2. Ideal Thermodynamic Processes

        The Magnetocaloric Effect can be understood, as mentioned above, via the isothermal and/or adiabatic processes; and these processes are characterized by the magnetic entropy change and the adiabatic temperature change, respectively. Below, we describe how these quantities are measured.

            2.1. Magnetic Entropy Change

        Consider the Helmholtz free energy F as a function of magnetic field and temperature, i.e., F=F(H,T). Thus, we can write:

equation 1

However, we know that:

equation 2

where S is the entropy and U=-MH stands for the internal energy (M is the magnetization). Thus, since we know that F=F(H,T):

equation 3

Comparing eqs. (1) and (3):

equation 4

After a small mathematical develompment, we finally arrive to the main equation that rules the Magnetocaloric Effect:

equation 5

To obtain the magnetic entropy change we just need to integrate the above equation:

equation 6

Thus, to obtain the magnetic entropy change we need to measure magnetization as a function of magnetic field and temperature, i.e., M(H,T). However, there is another way (less usual), to obtain the magnetic entropy change DS; i.e., from the specific heat. Let us start from the definition of specific heat:

equation 7

After integration we can also write the magnetic entropy change:

equation 8

 

                2.2. Adiabatic temperature change

        In a similar way as before, let us suppose that the entropy is a function of magnetic field and temperature S=S(H,T). Thus, we can write:

equation 9

Considering therefore the adiabatic condition dS=0 and equations (5) and (7), we found:

equation 10

which, after integration lead us to the adiabatic temperature change:

equation 11

Thus, in conclusion, to obtain the adiabatic temperature change, we need to measure M(H,T) and C(T,H). However, there is another way to measure this quantity, i.e., directly appling a magnetic field to the sample (adiabatically) and measuring the corresponding temperature change.

REFERENCES

[1] Warburg, Ann. Phys. (Leipzig) 13 (1881) 141

[2] Debye, Ann. Phys. 81 (1926) 1154

[3] Giauque, J. Am. Chem. Soc. 49 (1927) 1864

[4] Giauque, Phys. Rev. 43 (1933) 768

[5] http://www.universe.nasa.gov/xrays/programs/astroe/eng/adr.html

[6] Gschneidner, Rep. Prog. Phys. 68 (2005) 1479